# 第五章习题

# 习题 5.11

如图 5-67 所示多边形，若采用扫描转换算法 (改进的有效边表算法）进行填充，试写出该多边形的 ET 表和当扫描线 y=4 时的有效边表 (AET 表，活性边表）

# 第六章习题

# 习题 6.7

# 题目

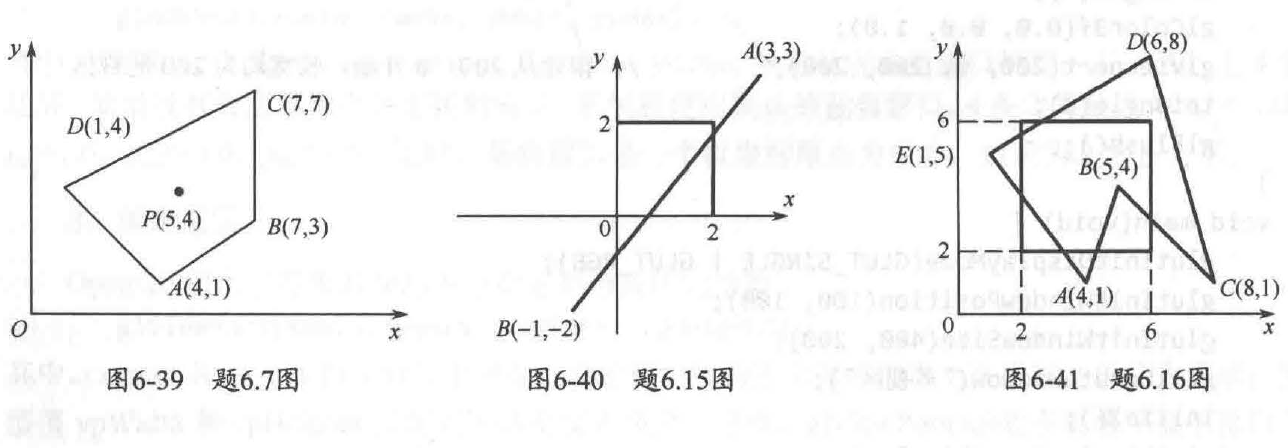
如图 6-39 所示四边形 ABCD, 求绕 P (5, 4) 点分别旋转 45° 和 90° 的变换矩阵，并求出各端点的坐标，画出变换后的图形。

# 解答

1. 先求变换矩阵

$$T=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -5& -4& 1 \end{bmatrix} \cdot \begin{bmatrix} cos90^\circ & sin90^\circ & 0 \\ -sin90^\circ & cos90^\circ & 0 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 5 & 4 & 1 \end{bmatrix} =\begin{bmatrix} 0 & 1 & 0 \\ -1& 0 & 0 \\ 9 & -1& 1 \end{bmatrix}$$

2. 求各点变换后的坐标

$$\begin{bmatrix} 4 & 1 & 1 \\ 7 & 3 & 1 \\ 7 & 7 & 1 \\ 1 & 4 & 1 \end{bmatrix} \cdot \begin{bmatrix} 0 & 1 & 0 \\ -1& 0 & 0 \\ 9 & -1& 1 \end{bmatrix} = \begin{bmatrix} 8 & 3 & 1 \\ 6 & 6 & 1 \\ 2 & 6 & 1 \\ 5 & 0 & 1 \end{bmatrix}$$

变换后的坐标为：$A'(8,3), B'(6,6), C'(2,6), D'(5,0)$

3. 绘制变换后的图形
   

# 习题 6.11

# 题目

试用编码裁剪法裁剪如图 6-40 所示线段。

# 解答

端点 A：$code1=1010$，端点 B：$code2=0101$

1. 既不满足$code1|code2=0$，也不满足$code1\&code2 \neq 0$
   端点 A 在窗口外，按顺序从低位开始检测
   倒数第 2 位为 1，因此计算与右边界的交点
   直线段的斜率为：$k=\dfrac{y_2-y_1}{x_2-x_1}=1.25$
   右边界交点的 y 坐标为：$y=y_1+k(x-x_1)=1.75$
   右边界交点的坐标为$(2,1.75)$，代替端点 A，$code1=0000$
2. 此后线段同样不满足上述 2 个条件，A 在窗口内，将 A、B 交换，按位检测$code1=0101$
   最后 1 位为 1，计算与左边界的交点为$(0,-0.75)$，代替端点 A，$code1=0100$
3. 仍不满足 2 个条件，A 在窗口外，按位检测$code1=0100$
   第 2 位为 1，计算与下边界的交点为$(0.6,0)$，代替端点 A 后，$code1=0000$
   满足$code1|code2=0$，可 “简取”，最终裁剪线段为$(0.6,0),(2,1.75)$

# 习题 6.15

# 题目

试用 Sutherland-Hodgman 算法对如图 6-41 所示的多边形进行裁剪，要求画出每次裁剪对应的图形，并标明输入和输出的顶点。

# 解答

1. 用左⬅️边界裁剪
   输入 ABCDE
   输出 12ABCD
2. 用下⬇️边界裁剪
   输入 12ABCD
   输出 1234B56D
3. 用右➡️边界裁剪
   输入 1234B56D
   输出 1234B7D
4. 用上⬆️边界裁剪
   输入 1234B7D
   输出 1234B789

# 习题 6.16

# 题目

试用 Weiler-Atherton 算法对如图 6-41 所示的多边形进行裁剪，要求写出每步裁剪的结果，并标明输入和输出的顶点，并与 6.15 题得到的裁剪结果进行比较。

# 解答

从 A 出发，按逆时针方向处理顶点

1. AB 段，输出$V_1B$
2. BC 段，可见侧进入不可见侧，输出$BV_2$，逆时针方向最近交点为$V_3$，输出$V_2V_3$
3. CD 段，不输出
4. DE 段，输出$V_3V_4$，转向，输出$V_4V_5$
5. EA 段，输出$V_5V_6$，转向，输出$V_6V_1$

# 第七章习题

# 习题 7.5

# 题目（第 1 问）

求将图 7-41 中空间四面体进行关于 P 点整体放大 2 倍的变换矩阵，写出复合变换后图形各顶点的规范化齐次坐标。

# 解答

1. 先求变换矩阵

$$T=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -2& 2 & -2& 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \frac{1}{2} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 2 & -2& 2 & 1 \end{bmatrix} =\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -1& 1 & -1& \frac{1}{2} \end{bmatrix}$$

2. 求各点变换后的规范化齐次坐标

$$\begin{bmatrix} 2 & 0 & 0 & 1 \\ 2 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -1& 1 & -1& \frac{1}{2} \end{bmatrix} =\begin{bmatrix} 1 & 1 & -1& \frac{1}{2} \\ 1 & 2 & -1& \frac{1}{2} \\ -1& 2 & -1& \frac{1}{2} \\ 0 & 2 & 0 & \frac{1}{2} \end{bmatrix}$$

$A'(2,2,-2,1), B'(2,4,-2,1), C'(-2,4,-2,1), D'(0,4,0,1)$

# 习题 7.7

# 题目

作出图 7-41 中空间四面体三视图，要求写清变换式（平移矢量均为 1）。

# 解答

1. 主视图

$$\begin{bmatrix} 2 & 0 & 0 & 1 \\ 2 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} =\begin{bmatrix} 2 & 0 & 0 & 1 \\ 2 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{bmatrix}$$

2. 俯视图

$$\begin{bmatrix} 2 & 0 & 0 & 1 \\ 2 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & -1& 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & -1& 1 \end{bmatrix} =\begin{bmatrix} 2 & 0 & -1& 1 \\ 2 & 0 & -2& 1 \\ 0 & 0 & -2& 1 \\ 1 & 0 & -2& 1 \end{bmatrix}$$

3. 侧视图

$$\begin{bmatrix} 2 & 0 & 0 & 1 \\ 2 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 0 & 0 & 0 & 0 \\ -1& 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ -1& 0 & 0 & 1 \end{bmatrix} =\begin{bmatrix} -1& 0 & 0 & 1 \\ -2& 0 & 0 & 1 \\ -2& 0 & 0 & 1 \\ -2& 0 & 1 & 1 \end{bmatrix}$$

4. 三视图如下：